Regression Analysis

変数間の関係性を基に予測

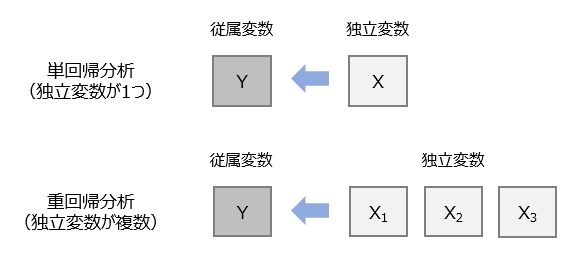
回帰分析は、2つ以上の変数の関係性をモデル化し、要因の影響を推定する手法です。また、モデル式を利用して従属変数（目的変数）を予測することができます。たとえば、販売数（Y）を売価（X1）と広告費（X2）の2つの要因で説明する場合、回帰分析を用いて、売価と広告費が販売数にどのような影響を与えるかを推定することができます。

独立変数が1つの場合は単回帰分析、独立変数が2つ以上の場合を重回帰分析と呼び区別します。従属変数および独立変数は、基本的にスケール変数を利用しますが、独立変数には2値変数やダミー変数に変換したカテゴリ変数を用いることも可能です。

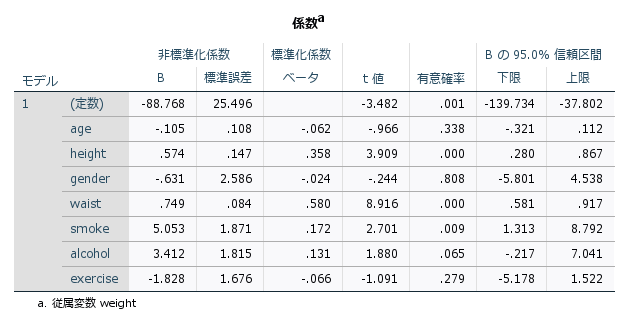
回帰分析の結果として得られる回帰係数（b）は、独立変数が従属変数に与える影響の大きさを示します。具体的には、ある独立変数が1単位変化したときに、従属変数がどれだけ変化するかを表します。例えば、価格（X）が1単位上昇すると、販売数（Y）がどれだけ減少または増加するかを回帰係数で解釈します。

また、重回帰分析の場合は、標準化係数によって従属変数に対してどの独立変数が重要かを識別することができます。回帰式の残差（residual）には正規性と等分散性を仮定するため、実際の分析では、残差の検討や決定係数による回帰式の説明力を確認することも重要です。

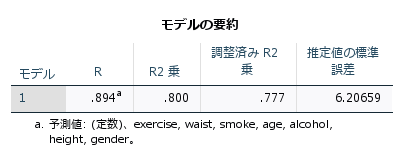
R2乗は、回帰モデルがデータのどれだけの変動を説明できているかを示す指標です。R2乗の値は、0から1の間で表され、1に近いほどモデルが従属変数をよく説明していることを意味します。ただし、R2乗は独立変数を増やすと増加するため、特に重回帰モデルでは調整済R2乗を用います。この指標は、モデルに含まれる独立変数の数とサンプルサイズに応じて調整したもので、過剰な変数を含むモデルを評価する際により適切な指標となります。

回帰分析は直線の式に要約するため、より正確には線形回帰分析と呼び、分散分析や共分散分析と同じく一般線形モデル（GLM）に含まれます。 相関係数が2つの変数の比例関係を示すのみであるのに対し、回帰分析の場合は一方からもう一方の変数を説明する関係性となります。さまざまな多変量解析の基礎となる手法で、応用範囲も広いです。

従属変数としてカテゴリ（質的）変数や生存時間を利用する場合は、ロジスティック回帰分析やCox回帰分析など別の手法が適用されます。

ソフトウェア

SPSSでは基本機能のBaseのみで回帰分析が可能です。Rでは基本的にstatsパッケージのlm()関数が最も利用され、視覚化にはggplot2、診断にはcarパッケージがよく使われます。Pythonでは機械学習ライブラリのscikit-learnが主に利用されますが、詳細な統計解析や診断が必要な場合はstatsmodelsが適しています。