Principal Component Analysis

類似する観測変数の合成

主成分分析（PCA, Principal Component Analysis）は、多次元データを低次元に圧縮し、データの特徴を抽出するための統計手法です。主に、高次元データの中から重要な情報を抽出し、データの構造を簡潔に表現する目的で使用されます。具体的には、複数の変数から構成されるデータセットを新しい軸（主成分）に変換し、その軸に沿ってデータを再配置します。これにより、元の変数の情報をなるべく多く保持しながら、次元数を減らすことができます。主成分は、元の変数の線形結合で表され、データの分散を最大化するように設計されています。

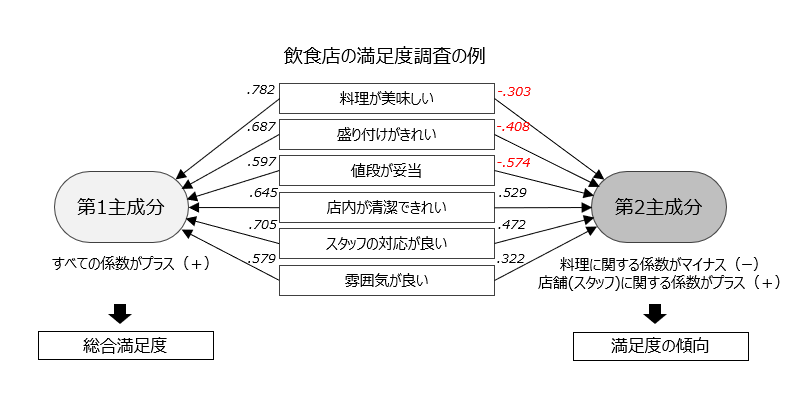
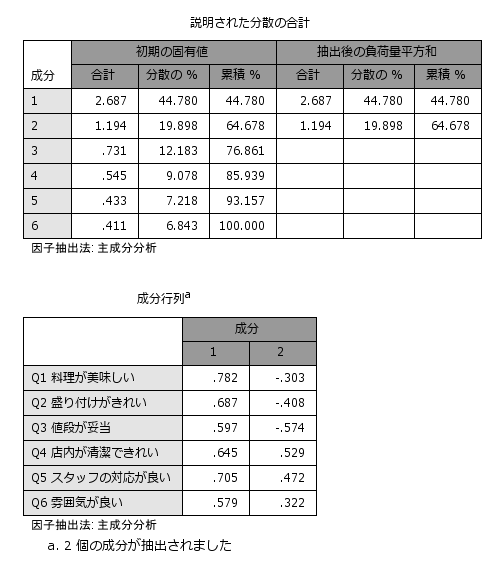
主成分分析を実行すると、各観測変数に重み（係数）が付けられ、主成分と呼ばれる合成変数が作成されます。最初に作られる主成分を第1主成分、次に作られる主成分を第2主成分と呼び、各主成分の構造を確認して分析者が名称をつけていきます。 第1主成分はすべての観測変数の係数がプラス（+）であるため、すべての項目の満足度が高い人ほど第1主成分の得点が高くなります。つまり、第1主成分は「総合満足度」を表していると解釈することができます。

第2主成分は料理に関する係数がマイナス（－）で、店舗やスタッフに関する係数がプラス（+）です。よって、第2主成分は、料理満足が高いか店舗満足度が高いかの「満足度の傾向」を表していると解釈することができます。

なお、このような主成分の解釈やネーミングは、分析者の仮説や知見、解釈の仕方やセンスなどによって大きく変わるため、上記の解釈はあくまでも一例です。

分析結果の視覚化

観測変数がたくさんあって解釈がしにくい場合、観測変数を少数の合成変数（主成分）に縮約することができれば、散布図などによる2次元の視覚化も可能となり、解釈がしやすくなります。この例では、6つの観測変数を2つの主成分に縮約しましたが、実際に主成分分析を行う場合は、各主成分の固有値や寄与率、累積寄与率などを確認しながら、できるだけ多くの情報を説明できるように主成分の数を検討します。

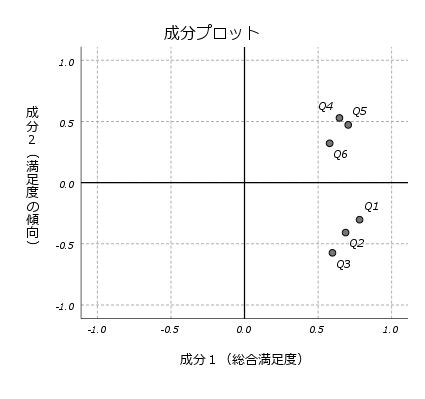
また、各主成分同士は無相関になる特徴があるため、相関の強い変数が多数ある場合に、最初に主成分分析を行い、その合成変数（主成分）を例えば回帰分析の独立変数に使用するという使い方もされています。主成分分析そのものは、従属変数を使用しない分類のための分析手法ですので、特に機械学習（マシンラーニング）の領域では、教師なし学習の手法に分類されます。 主成分分析は、観測変数同士の相関に基づいて変数を統合するため、量的変数（スケール変数）を使用しますが、量的変数とみなせる5件法や7件法などの順序尺度の変数もよく使用されています。

ソフトウェア

SPSSでは、Baseのみで実行可能です。分析メニューに主成分分析としてのメニューはなく、因子分析の計算方法の1つとして扱われています。Rでは、prcomp()やprincomp()を用いて主成分分析が行えます。可視化にはggbiplotやfactoextraといったパッケージも使用できます。Pythonでは、scikit-learnライブラリを使って実行可能です。