SPSSによるBland-Altman分析の手順
ASPSSの標準機能で行う方法
分析 > 記述統計 > ブランド・アルトマン分析
SPSS Statistics v30から、ブランド・アルトマン分析が標準機能として追加されました。使用する変数を選択し、必要な設定を選ぶだけで簡単にブランド・アルトマンプロットを作成することができます。標準機能を使用する場合は、変数名を日本語ではなくアルファベットとしてください。
なお、標準の機能ではプロット作成と一部の統計量の出力に対応しているものの、データセットに差分変数が作成されるわけではありません。プロットによる視覚的評価が目的の場合は標準機能が便利ですが、もし固定誤差や比例誤差の評価による補強も必要な場合は、事前に「差分変数」や「平均値変数」を作成する下記の手順に従うことをお勧めします。
12つの測定方法の差と平均値をあらわす変数の作成
グラフに使用する変数の作成
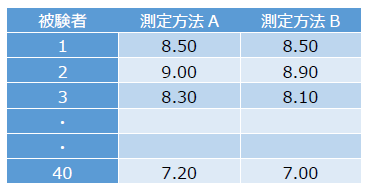
ブランド-アルトマンプロットは、横軸に2つの測定方法の差、縦軸に2つの測定方法の平均値をあらわします。グラフ作成の準備として、2つの測定方法の差の変数「DIFF」と2つの測定方法の平均値の変数「MMEAN」をデータセットに追加します。新しい変数の作成は、変数の計算メニューを利用します。
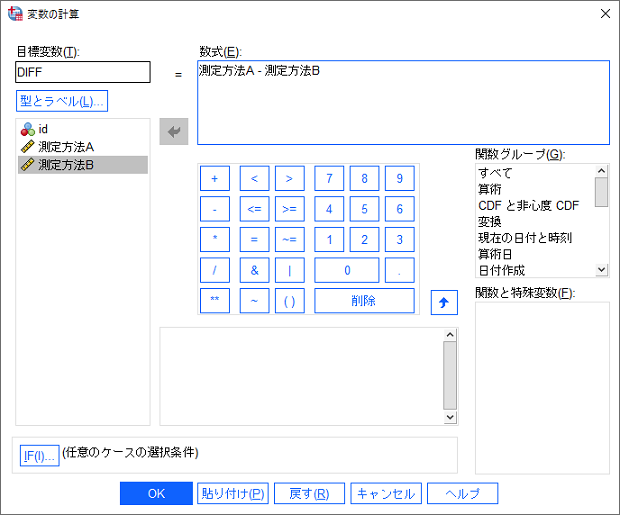
2つの測定方法の差
- 「変換」メニュー >「変数の計算」を選択します
- 「目標変数」に「DIFF」(任意の名前)と入力します
- 数式に2つの変数の差を求める式を入力します(例: 測定方法A-測定方法B)
- 「OK」ボタンをクリックします
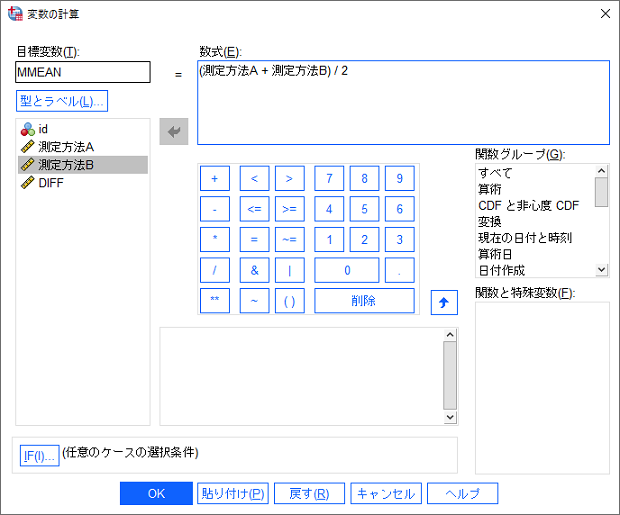
2つの測定方法の平均値
- 「変換」メニュー >「変数の計算」を選択します
- 「目標変数」に「MMEAN」(任意の名前)と入力します
- 数式に2つの変数の平均値を求める式を入力します(例: (測定方法A+測定方法B) / 2)
- 「OK」ボタンをクリックします
以上で、2つの測定方法の差をあらわす変数「DIFF」と、2つの測定方法の平均値をあらわす変数「MMEAN」がデータセットに追加されます。
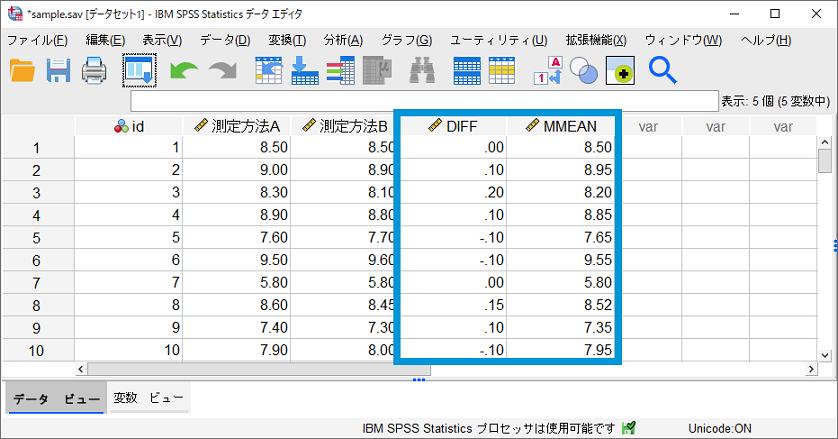
誤差の許容範囲(limits of agreement, LOA)を計算するために、「記述統計」でY軸(DIFF)変数の平均値と標準偏差を確認しておきます。
平均値と標準偏差の算出
- 「分析」>「記述統計」>「記述統計」を選択します
- 「DIFF」を変数ボックスに移動します
- 「OK」ボタンをクリックします

2つの測定方法の差の平均値が0.688、標準偏差が0.14083であることが確認できました。差の平均値が0に近いほど、2つの測定方法間のバイアスが小さいと解釈されます。例えば、2つの測定方法による値が完全に一致している場合、差の平均値は0になります。この値を中心に、差の平均値±1.96*標準偏差の範囲が誤差の許容範囲となります。
2ブランド-アルトマンプロットの作成
散布図の作成
次に、散布図の機能を利用してブランド-アルトマンプロットを作成します。ここでは「レガシーダイアログ」メニューを使用した手順をご紹介します。
散布図の作成
- 「グラフ」メニュー >「レガシーダイアログ」>「散布図」を選択します
- 「単純な散布」を選択し、「定義」ボタンをクリックします
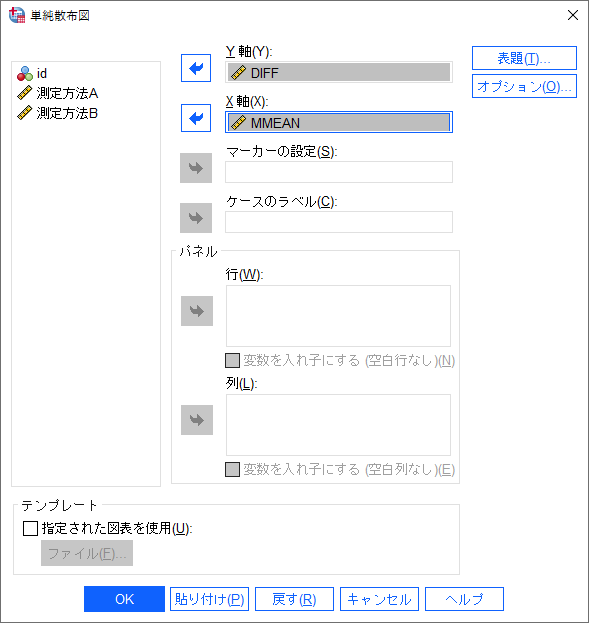
- 「Y軸」に2つの測定方法の差の変数(この例では「DIFF」)を指定します
- 「X軸」に2つの測定方法の平均値の変数(この例では「MMEAN」)を指定します
- 「OK」ボタンをクリックします
32つの測定方法の差(Y軸)の原点(0)を示す参照線の追加
Y軸の原点
固定誤差の有無を確認するために、Y軸の原点(0)をあらわす参照線を追加します。
Y軸に原点の参照線を追加
- 散布図をダブルクリックして、グラフエディタを起動します
- 「オプション」メニュー >「格子線の非表示」を選択します
- 「オプション」メニュー >「Y軸の参照線」を選択します
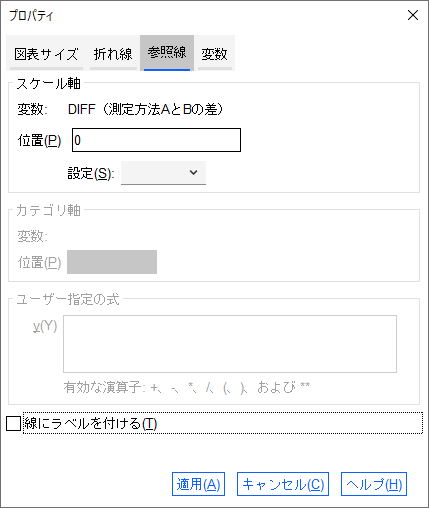
- プロパティダイアログボックスの「参照線」タブを開きます
- スケール軸の「位置」に「0」と入力します
- 「適用」ボタンをクリックします。
42つの測定方法の差(Y軸)の平均値を示す参照線の追加
Y軸の平均値
Y軸に平均値の参照線を追加
- 「オプション」メニュー >「Y軸の参照線」を選択します
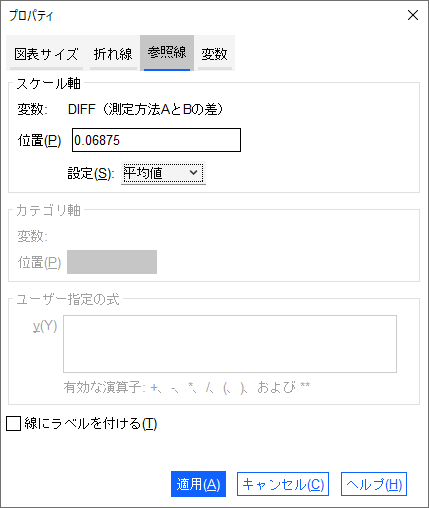
- プロパティダイアログボックスの「参照線」タブを開きます
- スケール軸の「設定」プルダウンリストから「平均値」を選択します
- 「適用」ボタンをクリックします
次に、原点(0)線と区別してグラフを見やすくするために線の種類を変更しておきます。
Y軸の参照線の線の種類の変更
- 「折れ線」タブを開きます
- 折れ線の「スタイル」のプルダウンリストから任意の線の種類を指定します
- 「適用」ボタンをクリックします
5許容範囲を示す参照線の追加
下限の参照線
許容範囲の下限は「差の平均値-1.96*差の標準偏差」で計算します。この例では、「-0.20723」(=0.0688-1.96*0.14083)となります。
下限の参照線の追加
- 「オプション」メニュー >「Y軸の参照線」を選択します
- プロパティダイアログボックスの「参照線」タブを開きます
- スケール軸の「位置」に「許容範囲の下限値」を入力します
- 「適用」ボタンをクリックします
- 「折れ線」タブを開きます
- 折れ線の「スタイル」のプルダウンリストから任意の線の種類を指定します
- 「適用」ボタンをクリックします
上限の参照線
許容範囲の上限の計算は「差の平均値+1.96*差の標準偏差」で計算します。この例では「0.344827」(=0.0688+1.96*0.14083)となります。
上限の参照線の追加
- 「オプション」メニュー >「Y軸の参照線」を選択します
- プロパティダイアログボックスの「参照線」タブを開きます
- スケール軸の「位置」に「許容範囲の上限値」を入力します
- 「適用」ボタンをクリックします
- 「折れ線」タブを開きます
- 折れ線の「スタイル」のプルダウンリストから任意の線の種類を指定します
- 図表エディタを閉じて、編集を完了します
以上の手順で、ブランド-アルトマンプロットが作成されました。X軸は2つの測定方法の平均値、Y軸は2つの測定方法の差をあらわしています。つまり、X軸が被験者間の測定平均値のばらつき、Y軸が2つの測定方法の差のばらつきとして解釈することができます。
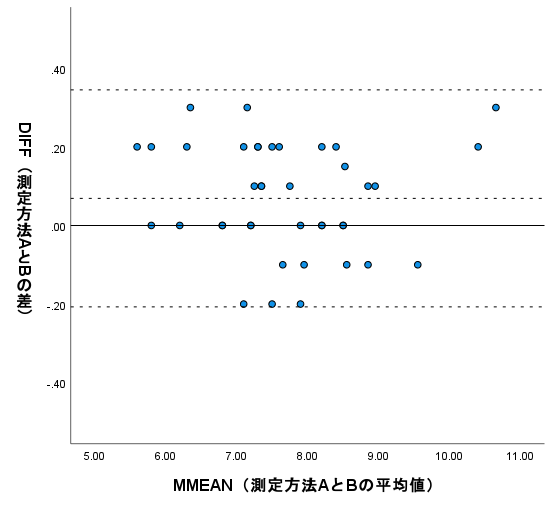
プロットは、Y軸の0よりやや上側にばらついているように見えます。つまり、測定方法Aよりも測定方法Bの方がやや小さく測定されており、固定誤差の存在が示唆されます。プロットはランダムにばらついており、比例誤差はなさそうです。
プロットは誤差の許容範囲(LOA)内でランダムにばらついていますので、2つの測定方法の一致性は高そうです。ただし、固定誤差が存在しますので、新しい測定方法Bを調整して偏りを補正することで、従来の測定方法Aと同等の結果を得ることができそうです。
6t検定による固定誤差の評価方法
固定誤差の評価
固定誤差は、t検定を利用して確認することができます。2つの測定方法の差の平均が0であるかどうかを、有意確率や差の95%信頼区間(Confidence Interval, CI)に基づいて評価します。
t検定
- 「分析」メニュー >「平均の比較」>「1サンプルのt検定」を選択します
- 「検定変数」に2つの測定値の差の変数(この例ではDIFF)を指定します
- 「OK」ボタンをクリックします


1サンプルの検定テーブルに、t検定の結果が出力されます。有意確率はp=0.004(p < 0.05)で有意差が認められます。差の95%信頼区間は0.0237~0.1138であり、区間内に0を含みません。区間内に0を含まない場合、2つの測定値の差が正または負の一方向に分布していることを示すため、固定誤差の存在が示唆されます。なお、元の測定値の変数を使用したt検定は、「記述統計」メニュー >「平均の比較」> 対応のあるサンプルのt検定」から実行可能です。
7回帰分析による比例誤差の評価手順
比例誤差の評価
比例誤差は、回帰分析や相関分析を利用して確認することができます。比例誤差が存在する場合、ブランド-アルトマンプロットはX軸の増減に比例してY軸も増減する分布が示されますので、2つの変数間に有意な関係性が認められるかを確認します。ここでは、回帰分析を利用して確認してみます。
t検定
- 「分析」メニュー > 「回帰」>「線型」を選択します
- 「従属変数」に2つの測定方法の差の変数(この例ではDIFF)を指定します
- 「独立変数」に2つの測定方法の平均値の変数(この例ではMMEAN)を指定します
- 「OK」ボタンをクリックします
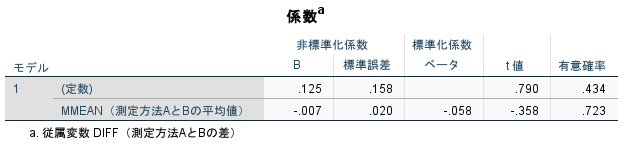
係数テーブルに、回帰係数の有意性検定の結果が出力されます。有意確率はp=0.723で有意差は認められません。つまり、回帰式に含まれる回帰係数が0であることを否定できませんので、比例誤差は存在するとはいえないと解釈することができます。
8比例誤差が存在する場合の一致性の評価
視覚的な評価
誤差の許容範囲(LOA)は測定範囲全体で測定値の差が変化しないことを想定しています。たとえば、測定値によって測定値の差の大きさが変化するような(比例誤差が含まれる)場合は、測定値の大小によってLOAが必要以上に広くなったり狭くなったりしてしまいます。
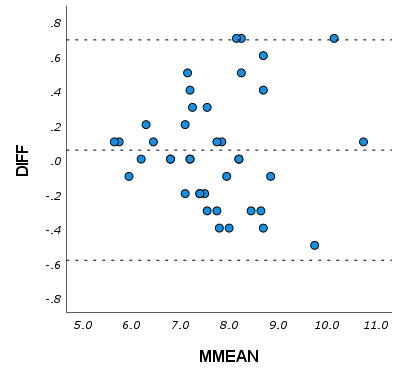
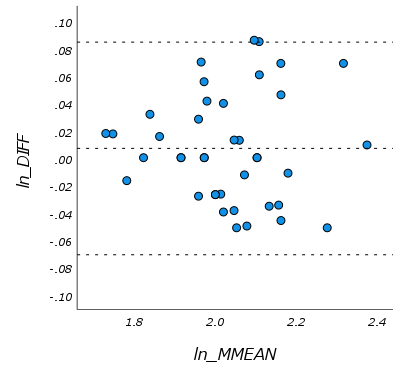
このような場合は、元の変数を対数変換(ln)し、再度ブランド-アルトマンプロットを作成する方法があります。ただし、対数変換を行う際は、変換後のデータに基づいて分析結果を解釈する必要があり、元の尺度に戻して結果を解釈する際には注意が必要です。対数変換が常に解決策であるわけではないこと、また変換を行う際にはデータの特性をよく理解し、適切な解釈が必要であることを明示することが望ましいです。
参考文献
- Bland JM, Altman DG. “Statistical methods for assessing agreement between two methods of clinical measurement.” Lancet. 1986;1(8476):307-10.
https://pubmed.ncbi.nlm.nih.gov/2868172/ - Bland-Altman plot
https://en.wikipedia.org/wiki/Bland-Altman_plot - Bland-Altman分析とlimits of agreementと思い出
https://triadsou.hatenablog.com/entry/2022/02/02/000727 - IBM_SPSS_Statistics_Base.pdf

