SPSS Statisticsによる傾向スコアマッチング
1傾向スコアの推定
ロジスティック回帰分析による予測値の保存
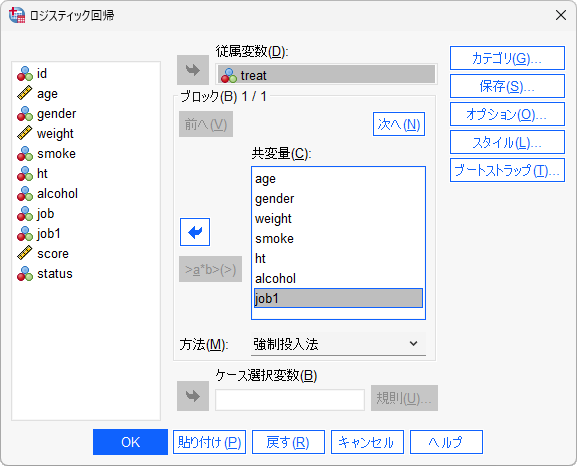
傾向スコアを推定する場合、従属変数に指定するのは、研究のアウトカムではなく2群への割付を表す変数です。例えば、treat(処置群/対照群)などが該当します。また、共変量には考えられる交絡因子をすべて投入します。下記は、Regressionオプションによるロジスティック回帰分析の手順です。
処置変数と共変量の指定
- 「分析」 > 「回帰」 > 「二項ロジスティック」を選択します。
- 「従属変数」に2群への割付を意味する変数を指定します。
- 「共変量」に2群への割付を説明するための説明変数(交絡因子)を指定します。
次に、傾向スコアに該当する予測確率を変数として保存する設定を行います。
傾向スコア変数の保存の設定
- 「保存」ボタンをクリックします。
- 「予測値」の「確率」を選択します。
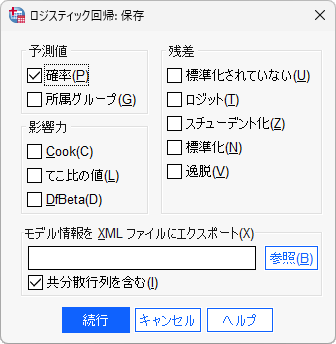
予測値の「確率」のチェックボックスを入れると、ロジスティック回帰モデルによる予測値が新しい変数としてデータセットに書き込まれます。これが、処置群に割り付けられる確率を意味する傾向スコアになります。
ロジスティック回帰分析の実行
- 「続行」ボタンをクリックします。
- 「OK」ボタンをクリックして、分析を実行します。
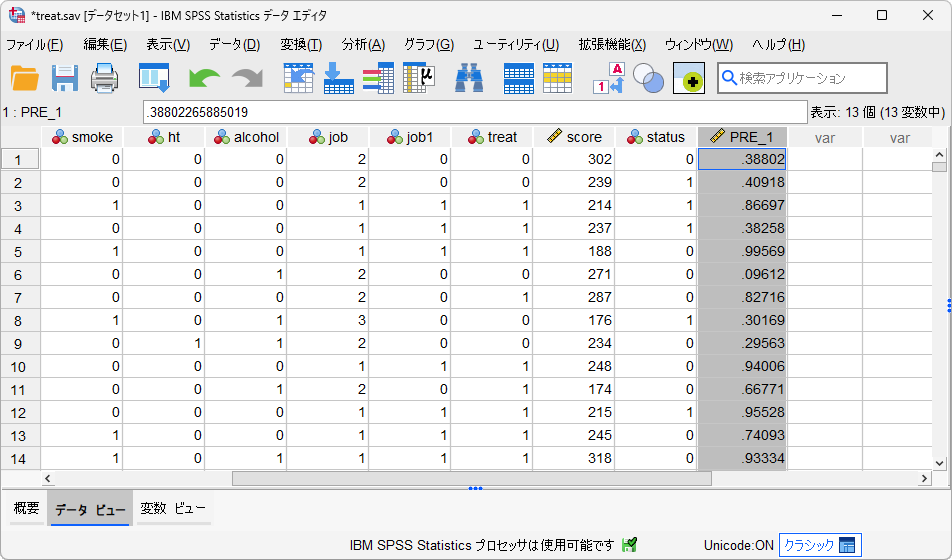
データビューの右端に追加される新変数「PRE_#」(#は実行の順番)が予測確率を保持しており、2群の割付変数を従属変数とした分析の場合、傾向スコアに該当します。この変数名は「PS」や「傾向スコア」などのように変更しておくと後の操作がより分かりやすくなりますが、この例ではこのままマッチングの手順に進めます。
傾向スコアの推定を行った後は、グラフによる視覚化や、ROC曲線によるAUC(c統計量)等によって傾向スコアを評価する手順が重要ですが、ここでは評価を完了している前提でマッチングの手順に進みます。
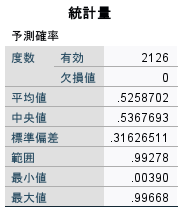
マッチング時に指定するキャリパーの設定として、傾向スコアの標準偏差を用いる基準がありますので、記述統計などで確認しておきましょう。
2傾向スコアマッチング
ケースコントロールの一致
傾向スコアの推定が完了していますので、次に傾向スコアに基づいて処置群と対照群をマッチングします。これには、「ケースコントロールの一致」メニューを使用します。マッチングは、処置群と対照群の間で傾向スコアが近いケースをペアにしてバイアスを減らす方法です。
ケースコントロールの一致による傾向スコアマッチング
- 「データ」 > 「ケースコントロールの一致」を選択します
- 「一致させる変数」に傾向スコア変数を移動します
- 「適合の許容度」を入力します
- 「グループインジケーター」に処置変数を移動します
- 「ケースID」にケース識別のための変数を移動します
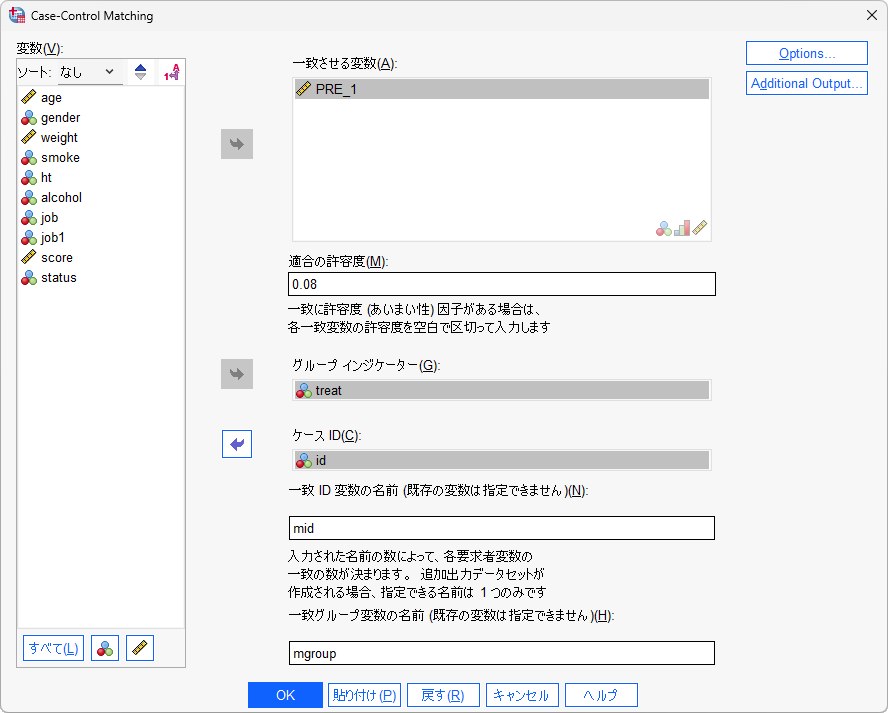
適合の許容度 : マッチング対象とするケースの傾向スコアのずれの上限(キャリパー)を指定します。この値を大きくするとマッチングされるケースが増え、値を小さくするとマッチングされるケースが減ります。この値の目安として、傾向スコアの標準偏差の0.2倍や0.25倍が推奨されています。この例では、0.08を指定していますが、これは傾向スコアの標準偏差を0.25倍で求めた値(この例では、0.3126511*0.25=0.079066)です。この値をブランクにすると完全一致のマッチングになります。
グループインジケーター : 2群への割付を意味する説明変数を指定します。数値型(0/1など)である必要があり、文字型(対照群/治療群など)は使用できません。
一致ID変数の名前 : マッチングによって一致したIDを記録するための任意の変数名を入力します。
一致グループの変数名 : 一致グループのコード値を保持する任意の変数名を入力します。値自体に意味はなく、同じ値を持つ2つのケースがペアを意味します。
乱数シードの設定
- 「Options」ボタンをクリックします
- 「乱数のシード」に任意の数値(例えば、123)を入力します
- 「Match Quality Meas…」の「Absolute Value」を選択します
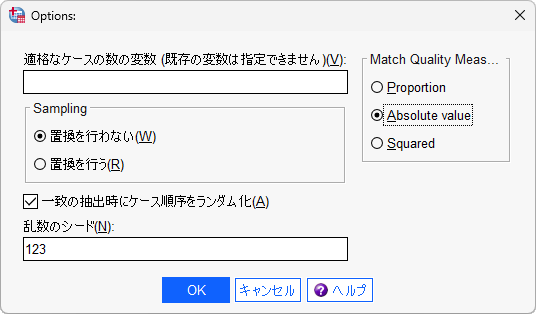
乱数のシードを明示的に指定することで、同一データにおけるマッチング結果の再現を保証できます。シードの指定がない場合、マッチングを行うたびに異なる結果になる可能性があります。シードの値は結果の再現に必要となりますので、必ず控えておきましょう。
Match Quality Meas…は、マッチングのペアを選択する際の基準の設定です。「Absolute Value」は、処置群と対照群の傾向スコアの絶対値の差を使用する設定です。この設定は、傾向スコアの絶対値の差が最小となるペアを選択するため、傾向スコアの近いケースがマッチングされることを意味します。
Samplingは、マッチングされる対照群のケース選択に重複を許さない非復元 without replacement と、重複を許す復元 with replacement の2つの指定です。この例では、非復元を選択しています。
データセット保存の設定
- 「OK」ボタンをクリックして、Option画面を閉じます
- 「Additional Output」ボタンをクリックします
- 「一致の新規データセットの作成」を選択し、任意のデータセット名を入力します
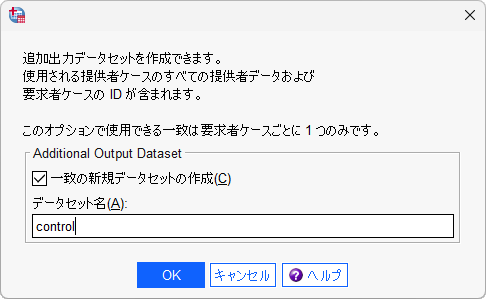
「一致の新規データセットの作成」を有効にすると、マッチングされた対照群を含むケース(この例では「mid」に記録されるID)を含むデータセットが作成されます。 データセットの名称は「control」(任意)としました。
傾向スコアマッチングの実行
- 「OK」ボタンをクリックして、Additional Output 画面を閉じます
- 「OK」ボタンをクリックして、マッチングを実行します
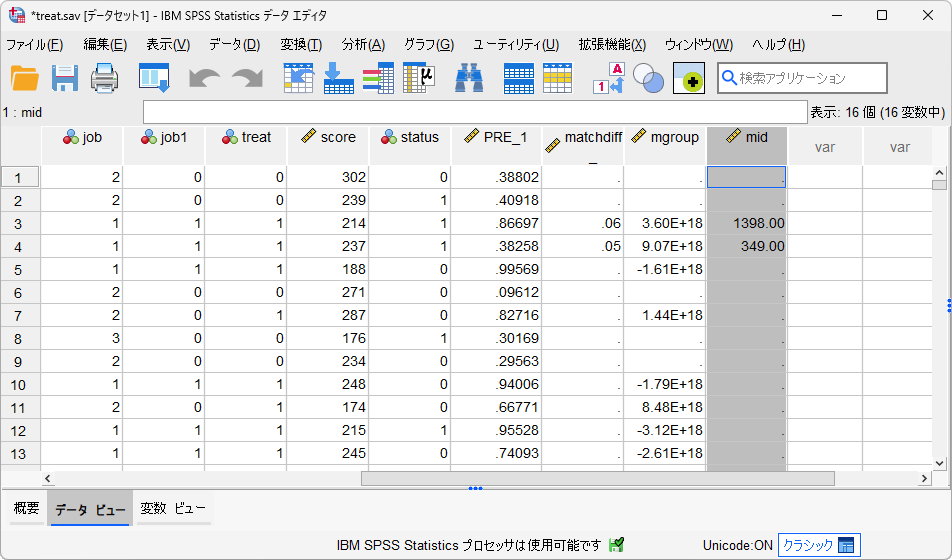
以上の手順で、傾向スコアが近いケースがマッチングされ、マッチングに成功した場合はその対象のIDが新しい変数(この例では「mid」)に追加されます。マッチング対象が見つからなかったケースは欠損値となります。
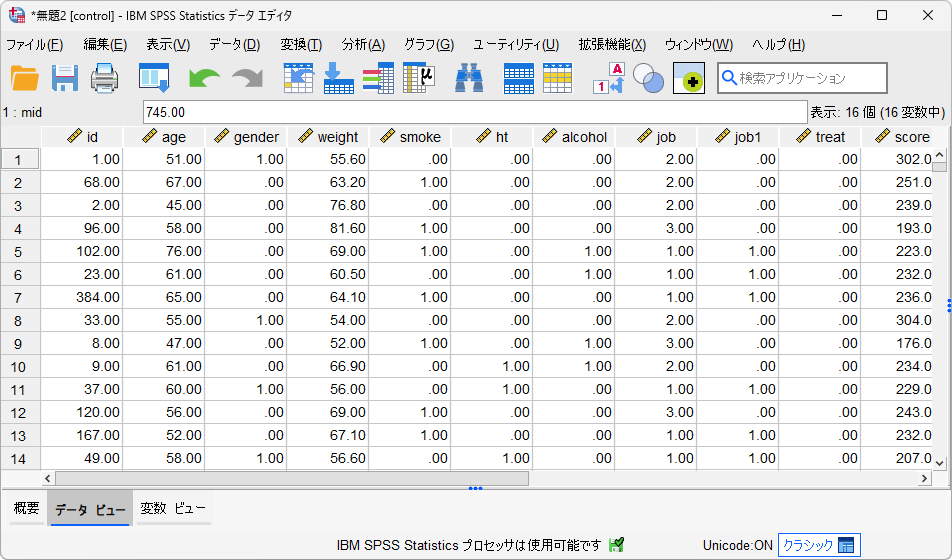
また、新しく作成されたデータセット(この例では「control」)をアクティブにして確認してみると、マッチング対象となった対照群のデータが保持されています。
最後に、条件抽出とファイル結合の方法で、マッチング対象が見つかった処置群のケースとマッチング対象になった対照群のケースを統合し、マッチングに成功した全ケースを含む新しいデータセットを作成します。
3マッチングデータファイルの作成
ケース選択とファイル結合
ケースコントロールの一致後のデータファイル(「treat.sav」)について、「mid」にマッチング対象のIDが記載されている(=欠損値ではない)ケースのみに絞り込みを行います。欠損値の判定は、MISSING関数を使用します。
ケースの選択
- 「データ」メニュー > [ケースの選択]を選択します。
- 「IF条件を満たしたケースを含む」を選択して「IF」ボタンをクリックします
- 「MISSING(mid)~=1」と入力します
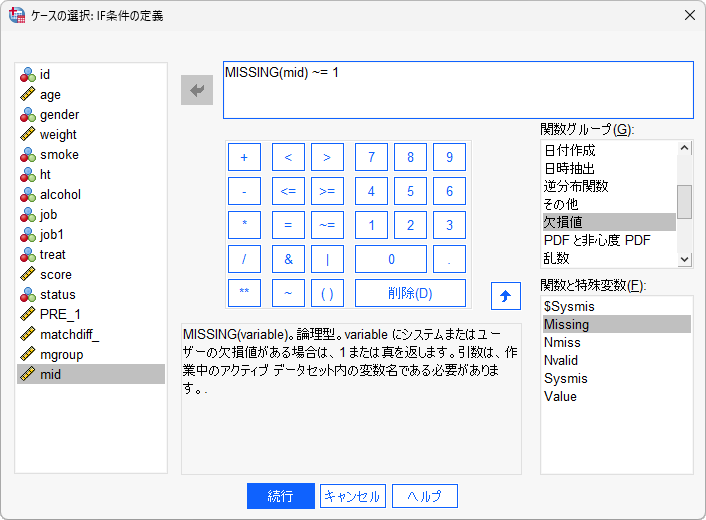
MISSING 関数は、指定した変数に欠損値が含まれるかどうかを判定することができ、欠損値の場合に1または真を返します。「~=」はSPSS Statisticsでノット―コールを意味する記号です。MISSING(mid)~=1は、midが欠損値ではないという意味になり、欠損値ではないケースを抽出する場合によく用いられます。
ケースの選択
- 「続行」ボタンをクリックします
- 「選択されたケースを新しいデータセットにコピー」をクリックします
- 「データセット名」に任意のデータセット名を入力します
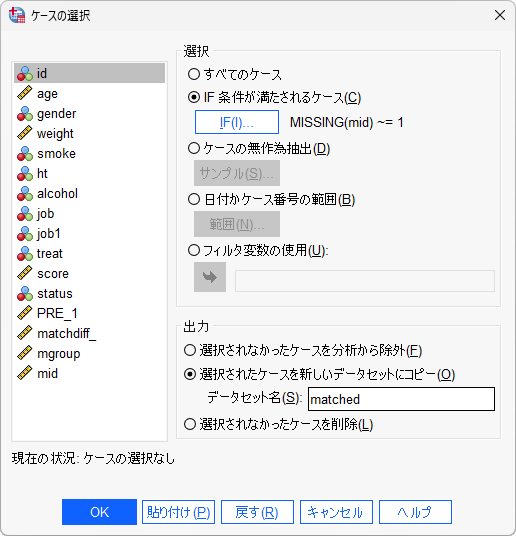
以上の設定で、「mid」が欠損値でない(=マッチング対象のIDが記録された)ケースのみのデータセット(この例では「matched」)が作成されます。
ケースの選択
- 「OK」ボタンをクリックします
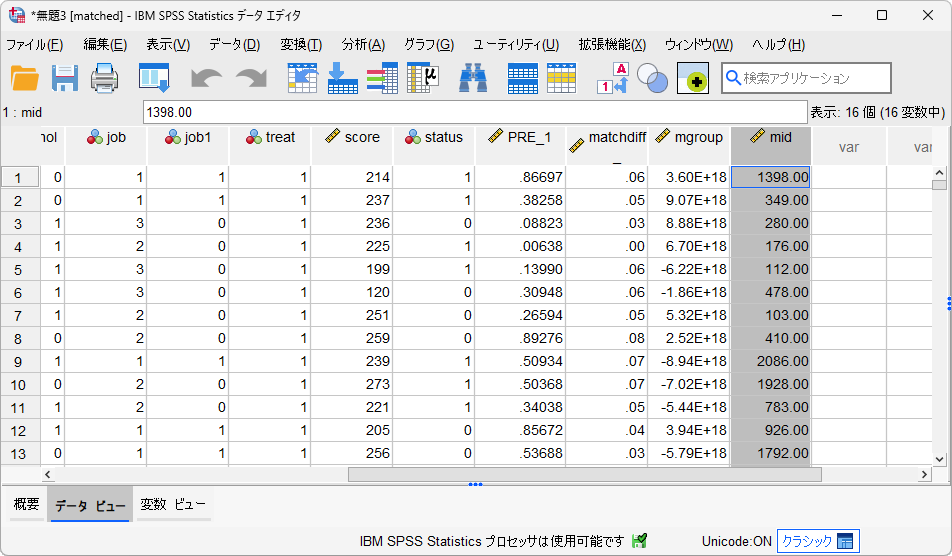
ケースの絞り込みが行われ、midが有効なケースのみが残りました。これはマッチング対象が見つかった処置群のデータを抽出したものです。
このデータセットに、マッチング対象となった対照群のケースが記録されているデータセット(「control」)を統合し、1つのデータファイルにまとめます。この手順は、ファイル結合のケースの追加機能を使用します。
処置群と対照群のファイル結合
- 「データ」 > 「ファイルの結合」 > 「ケースの追加」を選択します
- 「開いているデータセット」を選択し、マッチング対象となるケースのデータが記録されているデータセット(この例では、無題2[mpair])を選択します。
- 「続行」ボタンをクリックします
- すべての変数が「新しいアクティブなデータセットの変数」に移動していることを確認します
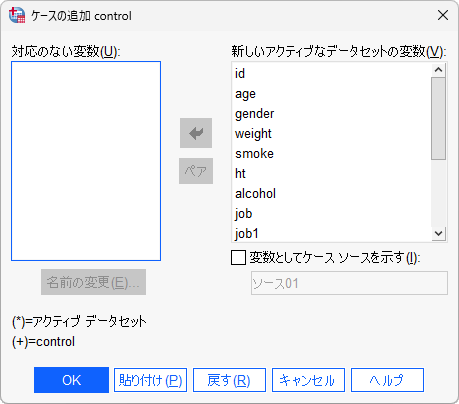
処置群と対照群のファイル結合
- 「OK」ボタンをクリックして、ケースの追加を実行します
以上の手順で処置群と対照群をマッチングした新たなデータセットが作成されました。傾向スコア(処置群に割り付けられる確率)が近いケースがマッチングされたことで、背景情報のバランスが調整されていると考えます。
4結果の確認
傾向スコアの分布や背景情報の確認
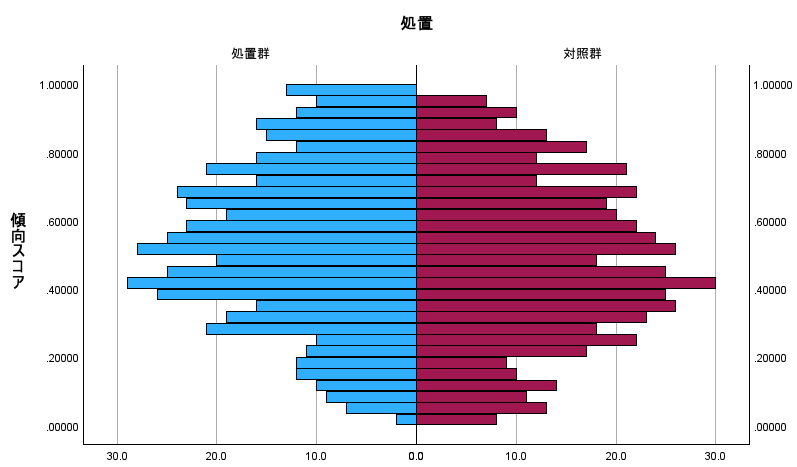
傾向スコアを処置群と対照群で比較するヒストグラムを作成すると、以下のように各スコアの分布が確認できます。
また、背景変数の平均値の比較を行うと、処置群と対照群のバランスが取れているかどうかを確認することができます。実際には、標準化平均差(SMD)やラブプロットなどで比較を行いますが、ここでは省略します。
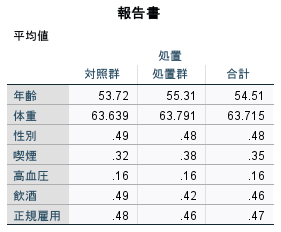
傾向スコアマッチングの目的は、比較する2群の背景情報のバランシングです。共変量が均一になったことが確認できたら、t検定などの単純な手法で処置効果を推定することができます。
参考文献
- Rosenbaum, P. R., & Rubin, D. B. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika, 70(1), 41-55.
- Austin, P. C. (2011). An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies. Multivariate Behavioral Research, 46(3), 399-424.
- Shenyang Y. Guo(著),Mark W. Fraser(著)『Propensity Score Analysis: Statistical Methods and Applications』SAGE Publications, Inc(2009)
- 星野崇宏(著)『調査観察データの統計科学 因果推論・選択バイアス・データ融合』岩波書店(2012)
- 新谷歩(著)『今日から使える医療統計』医学書院(2015)
- 中室牧子、津川友介(著)『「原因と結果」の経済学』ダイヤモンド社(2017)
トレーニング


