適合度指標 Standardized RMR の出力
Standardized Root Mean square Residual
IBM SPSS Amosでは、主要な適合度指標が自動的に出力されます。代表的な適合度指標として、GFI(Goodness Fit of Index)、AGFI(Adjusted Goodness of Fit Index)、CFI(Comparative Fit of Index)、RMSEA(Root Mean Square Error of Approximation)などがあります。RMR(Root Mean square Residual)は、モデルの分散共分散行列と観測データの分散共分散行列の平均的な差を指標化したもので、値の下限値である0に近いほど適合が良いと判断します。
ただし、RMRは標準化されていないため、GFIやAGFIのように基準となる目安を考えることが困難です。そこで、標準化したSRMR(Standardized Root Mean square Residual)が用いられる場合があります。SRMRでは0.05以下であれば良好で0.1以上で良くない適合と解釈する基準がよく利用されます。SRMRは、Amosでは自動で計算されないためプラグインメニューを別途使用する必要があります。
1プラグインメニュー
Standardized RMRの出力の準備
RMRは、Amosで推定値を計算すると自動的に算出され、Amos出力ウィンドウの「モデル適合」の欄にGFI、AGFIとともに一覧で表示されますが、SRMRは標準機能として用意されていないため推定値の計算によって自動的には算出されません。
プラグインメニューの呼び出し
- 「ツール」メニューから「プラグイン」を選択します
- 「Standardized RMR」をクリックします
上記のStandardized RMRダイアログボックスが表示されますが、この時点ではボックス内には何も表示されていません。このボックスを表示させたままの状態で推定値の計算を実行することで、ボックス内に計算結果を表示させることができます。
2推定値の計算
Standardized RMRの出力
ダイアログボックスを表示したまま、推定値の計算を行います。推定値の計算を行うにはあらかじめモデル(パス図)に名前を付けて保存しておく必要があります。
Standardized RMRの出力
- 推定値の計算ボタンをクリックします
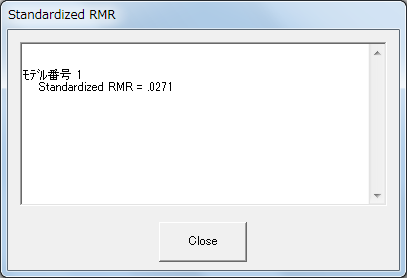
推定値の計算によって、空欄であったダイアログボックス内にSRMRが表示されます。SRMRでは0.05以下であれば良好で0.1以上で良くない適合と解釈する基準がよく利用され(そのほか、0.08以下であれば当てはまりが良いと判断する基準も利用されます)、この例では、SRMR=0.0271でありモデルの適合は良いようです。
このようにAmosではプラグインメニューによってSRMRの出力が可能です。ただし、推定値計算によって自動的に出力されるGFIやAGFIをはじめとするその他の適当度指標と異なり、SRMRはテキストマクロに対応していないため、パス図にSRMRの値を自動的に表示させることはできません。
また、SRMRはAmos出力ファイルにも書き込まれないため、ファイルを保存してもSRMRの値は保存されず、推定値を計算した後に画面上で確認するにとどまります。目的や使い方、用途に応じて、IBM SPSS Amosを有効にご活用ください。
参考文献
- IBM SPSS Amos User Guide.pdf
- 豊田秀樹, 共分散構造分析 [入門編], 東京図書,1998
- Hu, L. & Bentler, P. (1999). Cutoff criteria for fit indices in covariance structure analysis: conventional criteria versus new alternatives. Structural Equation Modeling, 6, 1-55.
- 豊田秀樹, 共分散構造分析 [Amos編], 東京図書, 2007
- 豊田秀樹, 共分散構造分析 [疑問編], 朝倉書店, 2011
- 平井明代, 教育・心理系研究のためのデータ分析入門-理論と実践から学ぶSPSS活用法, 東京図書, 2017

SPSS Q&Aサービス
無料体験

