SPSSによる傾向スコアによるマッチング

1マッチング前の2群の共変量の平均値

背景情報が等質ではない

以下は、ランダム化されていない観察研究のデータの例です。処置（介入群と対照群）の違いによって背景情報が異なります。例えば、介入群では高年齢層・喫煙者が多く、対照群では若年層・非喫煙者・高血圧・飲酒が多かったりするように背景情報がバラバラになってくると、治療効果が介入による影響なのか、年齢や喫煙、高血圧など背景要因の影響によるものなのかが分からなくなります。

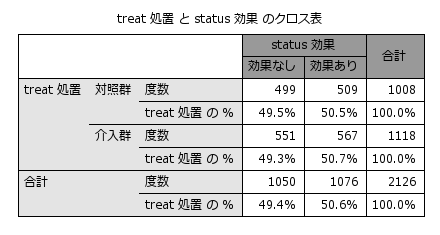
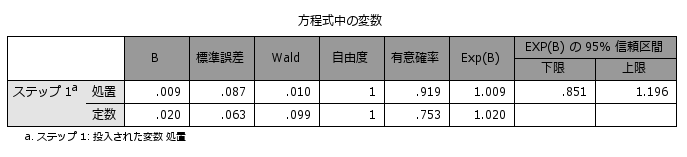
上記のような背景を持つデータで、独立変数（treat）によって効果（status）に違いがあるかを分析してみると、クロス集計表およびロジスティック回帰分析の結果から治療効果に2群の違いは認められず (対照入群＝50.5%、介入群＝50.7%、OR＝1.009 (0.851 to 1.196) )、介入による効果はなさそうですが、そもそも2つの群では背景となる年齢や性別、体重、喫煙、高血圧、飲酒、雇用形態など様々な要因に違いがみられるため、この分析結果を単純に受け入れるべきではなさそうです。

例えば、交絡因子が年齢のみであれば、同じ年齢層で比較するなどマッチングによるバランス調整も比較的容易ですが、交絡因子が多数の場合は単純なマッチングが困難です。そこで、複数の共変量を1つにまとめて得点化した変数(傾向スコア)を用いて、背景情報のバランスを調整するために用いるのが、傾向スコアによるマッチングです。傾向スコアによるマッチングを行うことで、介入の効果を単純に比較できる可能性が高まります。

傾向スコアの推定に用いられる代表的な分析手法は、ロジスティック回帰分析です。研究目的の本来のアウトカムではなく、2群への割付を意味する処置変数を従属変数、交絡要因となっている共変量を説明変数として用いたロジスティック回帰分析を実行して、介入群に割り付けられる確率を変数として保存します。

1傾向スコアによるマッチングの方法

「ケースコントロールの一致」と「傾向スコアによる一致」

SPSSで傾向スコアによるマッチングを行うメニューは大きく2種類があります。推奨されるのは、傾向スコアの推定とマッチングを個別に行うことができる「ケースコントロールの一致」メニューです。

「ケースコントロールの一致」推奨

このメニューでは、事前に推定した傾向スコアを用いてマッチングを行います。マッチング前に傾向スコアの評価やキャリパーの計算を行うことができます。また、傾向スコアの推定は、一般的なロジスティック回帰だけでなく、決定木分析、プロビット回帰、機械学習などの手法に対応します。実用的な観点から推奨されるメニューです。この機能は傾向スコア以外の共変量による古典的なマッチングにも対応します。手順の詳細はケースコントロールによる傾向スコアマッチングをご確認ください。

「傾向スコアによる一致」:

このメニューでは、傾向スコアの推定とマッチングが同時に行われるため、マッチング前に傾向スコアの評価やキャリパーの計算ができません。また、傾向スコアの推定はロジスティック回帰に限定されます。

2傾向スコアによるマッチングの手順

【注意】推奨されるメニューではありません

より推奨されるメニューとして、ケースコントロールによる傾向スコアマッチング をご参考ください。

マッチング前のデータセットを用意して以下の手順を行います。この方法は、傾向スコアの推定とマッチングが同時に行われるため、推定されたスコアの評価ができません。また、マッチング時に指定する許容の範囲(キャリパー)を求めることもできないため、傾向スコアの推定とマッチングは個別の手順で行うことを推奨します。

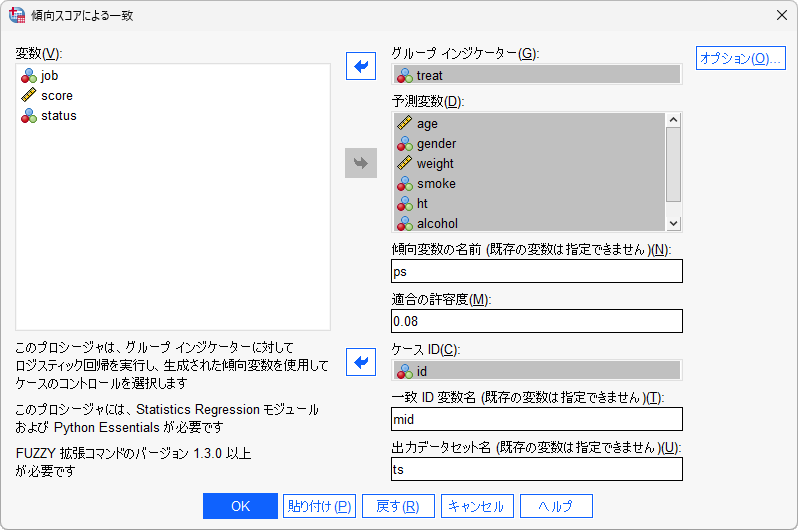
グループインジケーター : 2群への割付を意味する変数を指定します。
※数値型（0/1など）である必要があり、文字型（対照群/治療群など）は使用できません。
※分析の目的変数ではなく、処置変数を指定します。

予測変数 : 2群への割付を説明するための説明変数（交絡因子）を指定します。
※交絡として考えられる全ての共変量を指定します。

傾向変数の名前 : 保存される傾向スコア変数の任意の名前を入力します。

適合の許容度 : マッチング対象とするケースの傾向スコアのずれの大きさ（キャリパー）を指定します。この値を大きくするとマッチングされるケースが増え、値を小さくするとマッチングされるケースが減ります。
※傾向スコアの標準偏差の0.2倍や0.25倍が目安としてよく用いられます。

ケースID : ケース番号を特定する変数を指定します。

一致ID変数名 : マッチングによって一致したIDを記録するための任意の変数名を入力します。

出力データセット名 : マッチング後のデータセットの任意の名前を入力します。

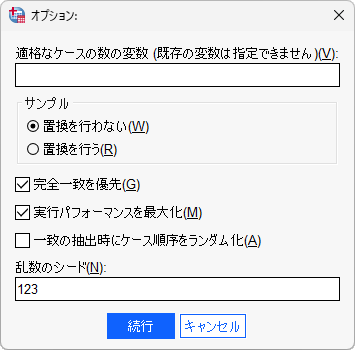
乱数のシードを明示的に指定しておくことで、同一データにおけるマッチング結果の再現を保証することができます。シードが指定されていない場合、マッチングを行うたびに異なる結果になる可能性があります。シードの値は任意の数値で問題ありませんが、指定した値は控えておく必要があります。

サンプルの置換を行わないは非復元(without replacement)マッチング、置換を行うは復元(with replacement)マッチングを意味します。通常は重複を許さない非復元マッチングを行います。

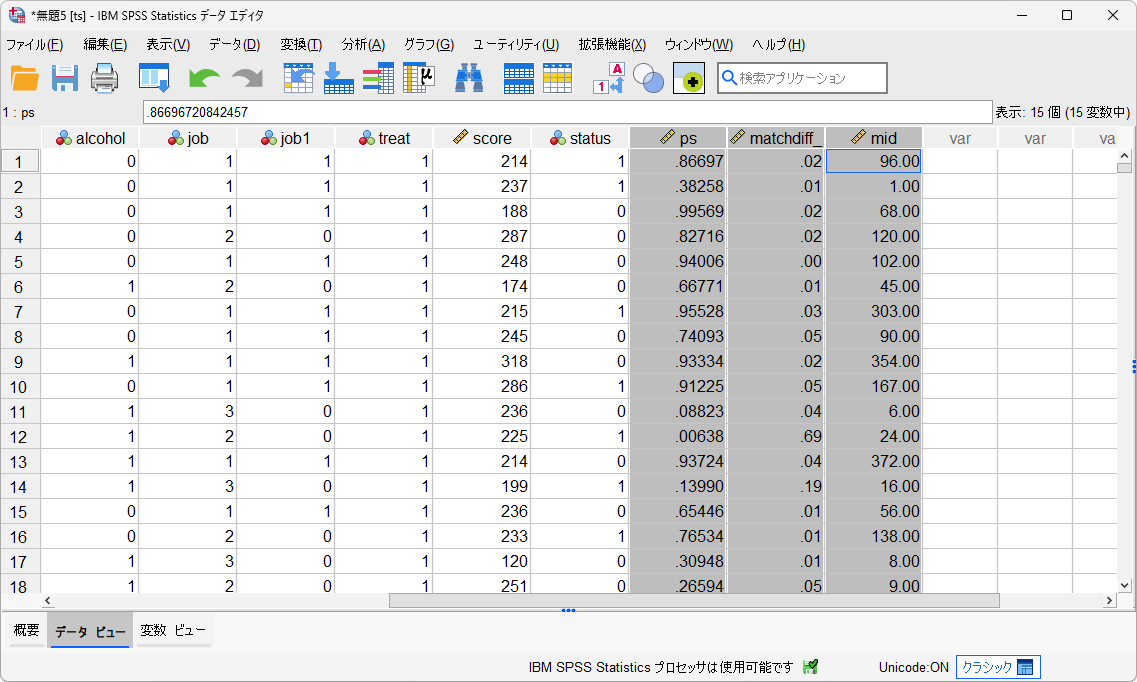
新しいデータセットが作成され、推定された傾向スコア(ps)とマッチングID(mid)が追加され、マッチングされたケースには対象のID番号が記録されています。「mid」が欠損値になっているケースは、マッチング対象がなかったケースです。

3マッチングされたケースの絞り込み

ケースの選択

次にマッチングされたケースのみに絞り込みを行います。マッチングに成功したケースは、マッチングIDが記録されているため、マッチングIDが欠損値でないケースを抽出することで、マッチングされたケースのみを含む新たなデータセットを作成できます。

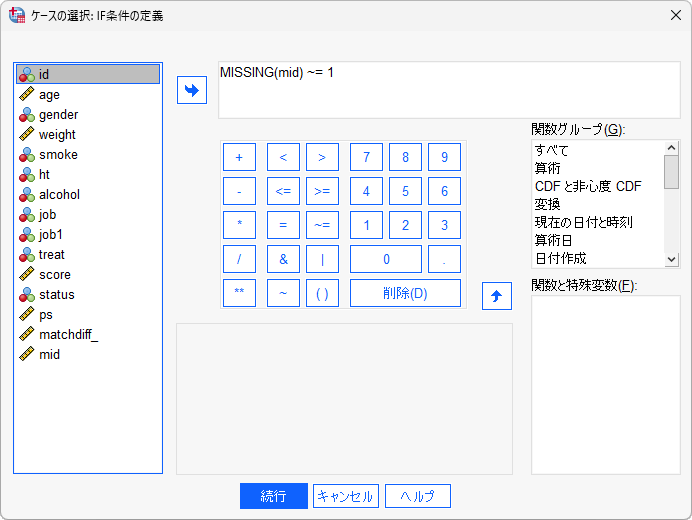
MISSING 関数は、指定した変数に欠損値が含まれるかどうかを判定することができ、欠損値の場合に1または真を返します。MISSING(mid)~=1は、midが欠損値ではないという意味になり、欠損値ではないケースを抽出する場合によく用いられます。

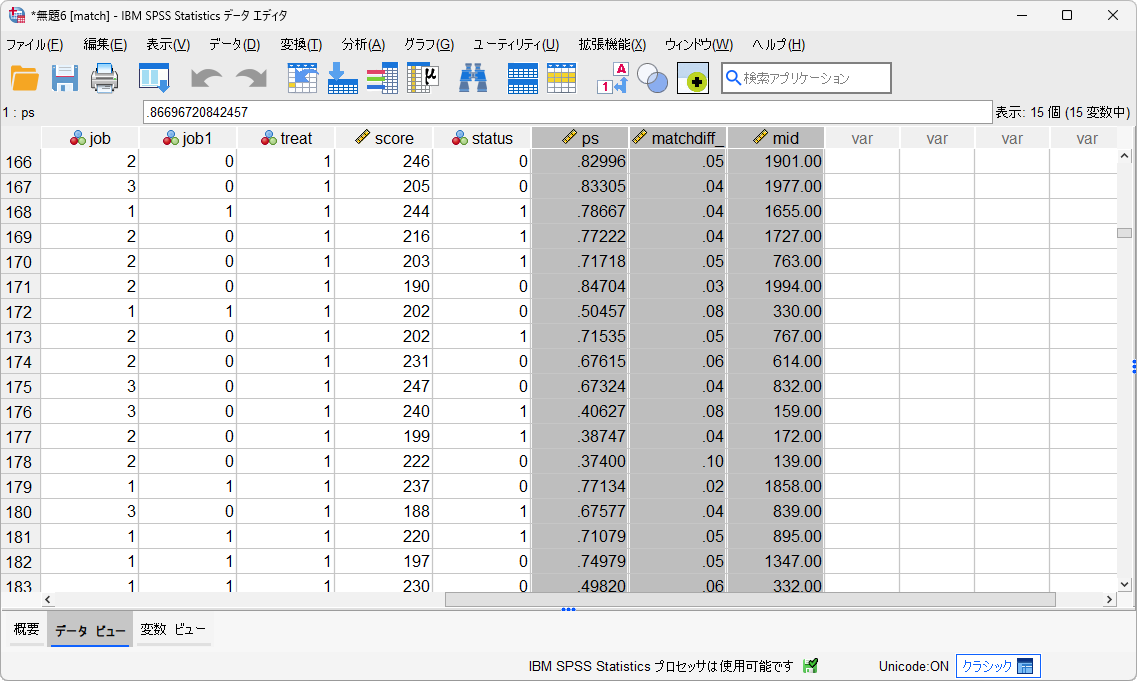
マッチングされたケースのみを含む新たなデータセットが作成されます。

4マッチング前の2群の共変量の平均値

背景情報が等質に近づく

マッチングされたデータセットで記述統計(探索的分析)を実行すると以下のような結果を得ることができます。処置の有無以外の背景情報がバランスされますので、単純に処置効果の推定を行うことができるようになります。

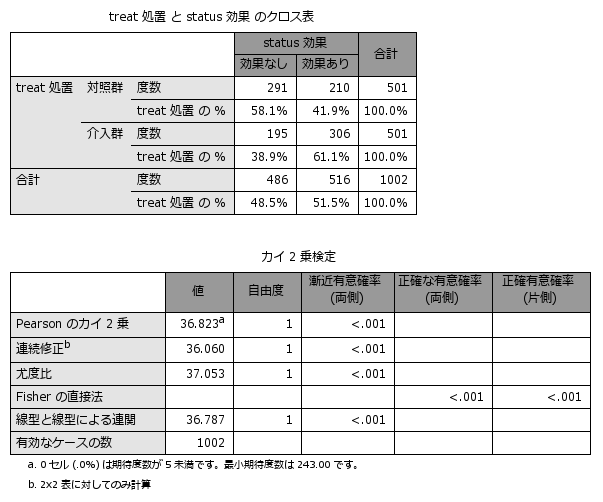
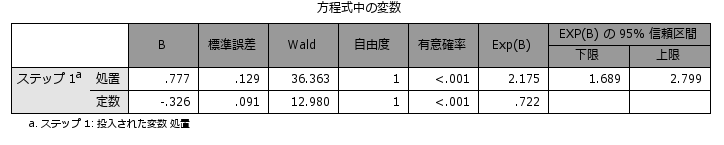
傾向スコアは、共変量を1つにまとめて背景情報のバランス調整に用いることができますが、観察されている共変量で調整を行いますので、観察されていない共変量での調整はできません。

また、マッチングを行うと、マッチングできなかったサンプルが分析から除外されることになりますので、最終的に使用できるn数が少なくなります。もともとn数が少ないデータを扱っている場合には、傾向スコアの推定自体ができなかったり、マッチングできるケース数が少なく分析できないなどの問題もあります。

観察型の研究において背景情報のバランシングを行うことで、あたかも無作為割り付けを行ったように単純に分析を行うことができるメリットがあります。